
図1:10つの観測点(緑の三角)の位置(平面図)。
例えば、図中の(10,20)はx=10km,y=20kmの座標に観測点があることを示す。 図中で、横軸がx、縦軸がy。

図1:10つの観測点(緑の三角)の位置(平面図)。
例えば、図中の(10,20)はx=10km,y=20kmの座標に観測点があることを示す。
図中で、横軸がx、縦軸がy。
【ステップ1】
波が到達した時刻を調べたら、下の図2のようになりました。
震源はどのあたりにあると考えられますか?
波が発せられたのはいつ頃でしょうか?
なぜそのように判断しましたか?
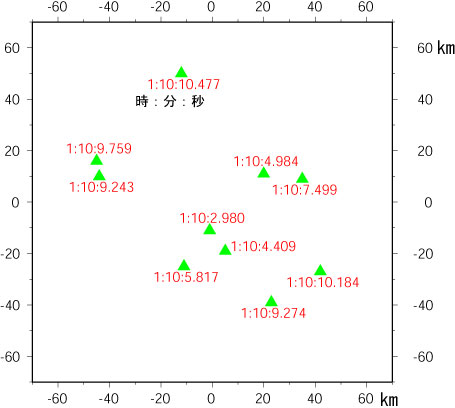
図2:波の到達時刻の観測値(赤字)。
例えば、図中の1:10:10.477は、1時10分10.477秒に観測点に波が来たことを示す。
【ステップ2】
仮の震源として、星印の場所を考えてみましょう。
この場所から波が発したとすると、地下の波の伝播速度がわかっていれば、
波の予測到達時刻を計算することができます。
その結果が、次の図3の青字です。
さて、仮の震源を本当の震源の位置に近づけるためには、
どのように動かしたらよいでしょうか?
なぜそのように判断しましたか?
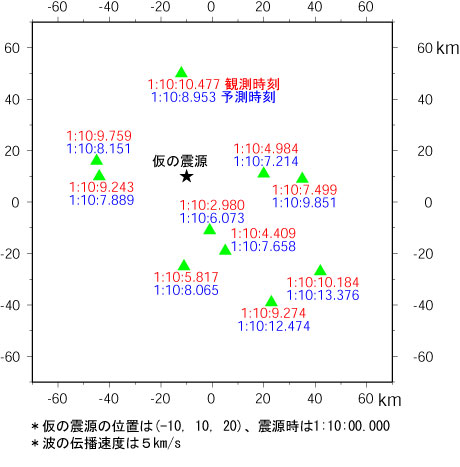
図3:到達時刻の観測値(赤字)と仮の震源に対する予測値(青字)。
仮の震源の位置は、黒の星印で示されている。
本演習では、 もっとも単純なケースとして、 均質な媒質の中で地震が起こり、その波の到達時刻を地表の観測点で 観測する場合を想定します。 行列Gは、一般的には、仮定した速度の分布をもとに波線追跡を行い 数値的に微分値を算出しますが、 均質媒質の場合には、解析的にえた式から微分値を計算できます。
均質な媒質では、波は観測点と震源を結ぶ直線で伝播します。 このとき、観測点に波が到達する時刻は、以下の式で与えられます。

作ろうとしているプログラムの流れは、 こちら です。
Pythonでプログラムを作成する場合には、 NumPyライブラリをimportすることで、各種の行列計算(逆行列の算出を含む)を行うことができます。
作ろうとしているメインプログラムの流れは、 こちら です。
Fortranでプログラムを作成する場合には、
逆行列は、次の2つのサブルーチンを使って計算できます(メインプログラムと同じところにダウンロードしてください)。
他の授業で使ったサブルーチンやライブラリがあれば、そちらを使っても構いません。
ludcmp.f
lubksb.f
上の2つのサブルーチンをメインプログラムの中で以下にように使うと、 n次の正方行列 a の逆行列が、正方行列 ainv に求められます。 (LU decompositionと呼ばれる方法を使っています) なお、npは配列の大きさを定義するための整数です。 npは n以上の整数であればよく、nと同じ値でも問題ありません。
---サブルーチンの使用例:ここから---
real:: a(np,np),ainv(np,np)
real:: dum
integer:: indx(np)
メインプログラムの部分
ainv=0
do i=1,n
ainv(i,i)=1
enddo
call ludcmp(a,n,np,indx,dum)
do j=1,n
call lubksb(a,n,np,indx,ainv(1,j))
enddo
メインプログラムの部分
---サブルーチンの使用例:ここまで---
ludcmp.f lubksb.fは、メインプログラムに付け加える必要は ありません(そうすると、逆にうまくいかないことがあります。) コンパイルするときに、メインプログラムのファイルといっしょに並べます。
例えば、da-main.f90というファイルがメインプログラムであるとしたら、
gfortran da-main.f90 ludcmp.f lubksb.f
./a.out
とすると、プログラムは動きます。