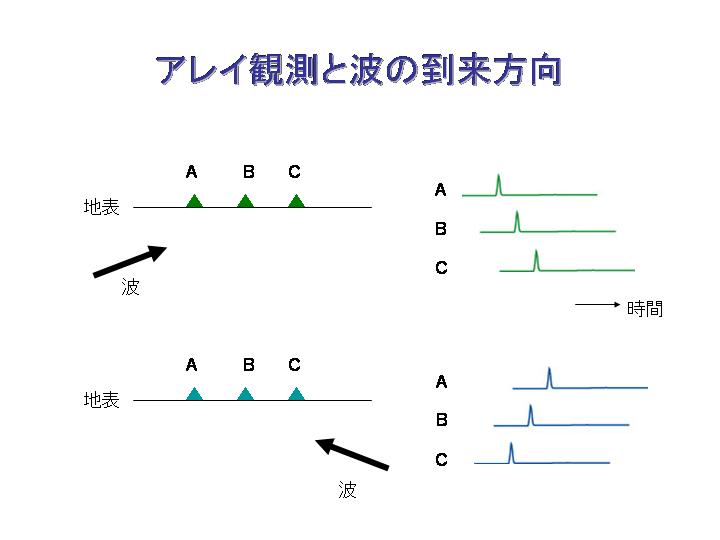
図1:波の伝播方向(左)とアレイ観測で記録される揺れのデータ(右)

図1:波の伝播方向(左)とアレイ観測で記録される揺れのデータ(右)
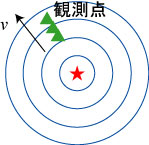
図2:円筒状に広がる波
図1のA点で波が到達する時刻は、距離AOをみかけ速度vで割った時刻(tA)となる。B点 に波が到達する時刻は、距離BOをみかけ速度vで割った時刻(tB)になる。 A点とB点での波の到達時刻の差は、これらの2つの時刻の差tB-tAとなっている。
これは、次のようにも、見ることができる。 観測点AとBの位置は地震計をおいたところなので、 わかっている。その位置を使って、震源Oの位置とvの値から、 (BO-AO)/v=tB-tAを計算できる。 観測点Bの記録を時間軸上にtB-tAずらしてやる。 すると、ずらした記録は観測点Aと同じになる。
この見方を利用して、未知数である「震源Oの位置」と「みかけ速度v」を
推測することができる。
(1) 震源の位置Oとみかけ速度vの値の候補として、Oiとviを仮定する。
(2) この仮定した値を使って、tB-tAの値を計算する。
(3) 計算された時間tB-tAだけBの記録をずらし、Aの記録と比べる。
もし同じならば、そのときのOiとviが真値の候補となる。
実際には、いろいろなOiとviの値を試みて、 ずらしたBの記録がもっともAの記録に似ているときのOiとviを推測値とする。
この演習では、実際に探索する量として、みかけ速度ではなく、 「みかけslowness」を使う。 slownessとは、速度の逆数のことである。 みかけ速度vのかわりに、みかけslowness sを使えば、観測点AとBの時間差は、 tB-tA=(BO-AO)sとなる。 つまり、 いろいろなOiと siの値を試みて、 ずらしたBの記録がもっともAの記録に似ているときのOiとsiを推測する ことになる。
また、観測点は2つである必要はない。多くの観測点であっても、 1つの観測点を基準点に設定すれば、それと各観測点の間で、 Oiとsiから時刻差が計算でき、その時間ずらした記録同士が似ているか 否かを、総合的に判断すればよい。
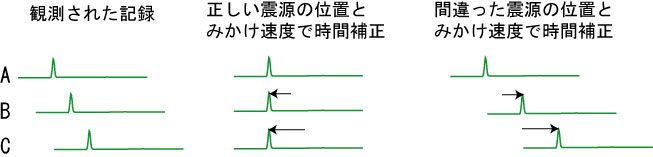
図3:正しい震源位置・みかけ速度を使って、観測データ(左)に
時間補正を施した波形(中央)と間違った値を用いた場合(右)
 式1:センブランスの定義式
式1:センブランスの定義式
波形が似ているとき、このセンブランスの値は大きくなる。 このセンブランスが大きくなる震源の位置とみかけ速度を探してみよう。
2つの観測点の間の距離は、前期の課題演習DAのように、 1つの観測点を基準にして、 そこから一度直交座標系に近似して計算してもよいが、 今回は、球面三角法をもとに、直接、緯度・経度の値から計算してみよう。
緯度と経度が与えられた2つの地点間の距離は、球面三角法に基づき、以下の 式で計算できる(例えば、宇津徳治「地震学 第3版」共立出版 p.84)
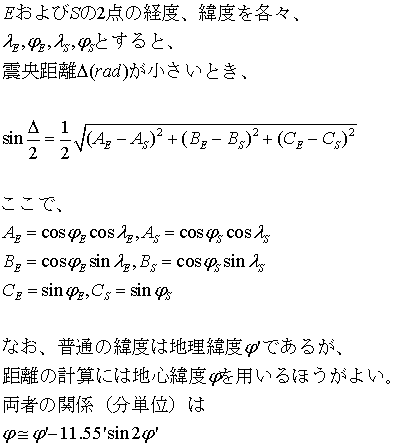 式2:距離の計算式
式2:距離の計算式
(2007年度HP資料より)