8月の阿蘇火山地震観測実習で、本堂のトンネルに 広帯域地震計を設置しました。実習の後も、その地震計はずっと 地震動をとり続けています。
10月25日深夜（日本時）、マグニチュードMw7.8の大地震が インドネシアのスマトラ島で起きました。 津波による被害が甚大で、400名を越える死者がでました。 "津波地震"であったのではないかと指摘する研究者もいます。
この地震は、 10月25日14時42分22秒（世界標準時）（日本時間では25日23時42分22秒）に 発生しました。 規模（マグニチュード）は、奥尻島に大きな津波被害をもたらした 1993年北海道南西沖地震（Mw7.7）より少し大きい程度です。
本堂の広帯域地震計は、この地震からのＰ波をきれいに記録しました。 ４回の演習で、そのＰ波の波形（"かたち"）をモデリングする（計算機上で 復元する）ことで、 地震の断層やずれの向き、断層のずれの継続時間や時間関数、震源の深さ などを推測・考察しましょう。
震源があるところでは、インド・オーストラリアプレートが北東に向かって ユーラシアプレートの下に沈み込んでいます。 スマトラ地震は、ユーラシアプレートとインド・オーストラリアプレートの プレート境界の地震と思われます。
本堂の震央距離は、 47° です。 震央距離が 30-100°の範囲を、地震学では「遠地（teleseismic distance）」と 呼んでいます。 この範囲のＰ波の波形は、 伝播するときに上部マントルやマントル遷移層の複雑な構造の影響を 受けにくいために、震源で起こったことを推測するときによく使用します。
地球の内部の速度構造を仮定すると、Ｐ波などの地震波が 伝播するにかかる時間を推測することができます。 "iasp91"という世界標準１次元速度モデルを用いると、 Ｐ波は本堂に506.05秒かかって到達し、 その後ＰＰ波が615.59秒かかって到達し、 Ｓ波は本堂に914.31秒かかって到達すると予想されます。 また、あわせて、 本堂に伝播するＰ波が、震源から鉛直下向きから上方に 28°の角度で射出したＰ波であることも推測されます。 （この角度を射出角take-off angleと呼んでいます）
地震の震源からみた本堂の方向（方位 azimuth）は、 37°、本堂からみた地震の震源の方向（逆方位 back-azimuth）は、-135°です。 いずれも、北をゼロとして時計回りを正に測られています。
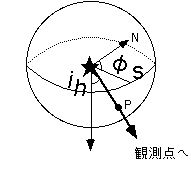★が地震、太い矢印が波の伝播方向、ihが射出角、φsが方位。
地動を見るためには、取得されたデータから、地震計の応答関数を 取り除く必要があります。 今回は、この作業を、SACというソフトウェアを使って行います。
阿蘇のデータがあるサーバにログインして、
作業を行ってください。
作業の詳細はココ
サーバへのログインやwin形式のデータを扱うコマンド等は、
第１回目の演習のメモにあります。
ココ
遠地P波の変位波形（変位の時間関数）は、波線理論をもとに、
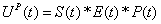
で、近似的に計算できます。
ここで、
S(t)は地震の断層運動によって決まる時間関数、
E(t)は地下構造によって生じる種々の波の到着を与える時間関数
（ここでは、直達P波とともに、震源そばの地表での
反射波や変換波を与える時間関数）、
P(t)は震源から観測点まで伝わる時の非弾性の効果を与える時間関数。
演習では、これらを計算するプログラムを作成します。
内容を説明するpdfノートはココ
【演習1】構造による時間関数E(t)を作る
【1-1】 断層運動から出るＰ波とＳ波の放射特性を計算する
断層の走向、傾斜角、すべり角（すべり方向）、Ｐ波の射出角と方位の５つの 変数を与えたときに、Ｐ波放射特性（Rp）を計算するプログラムをつくる。
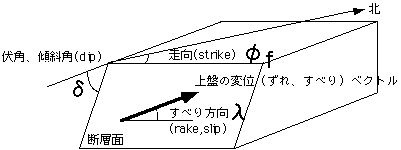
プログラムの動作確認として、
(1) 横ずれ断層（走向90°、傾斜角90°、すべり角0°）で射出角が45°のとき、 地震波の伝播する方位を0から360°まで増やしていった場合の Ｐ波放射特性（Rp）をgnuplotで図にしてみる。
(2) 逆断層（走向0°、傾斜角45°、すべり角90°）で 地震波の伝播する方位が90°のとき、 射出角を0から180°まで増やしていった場合のＰ波放射特性（Rp）を gnuplotで図にしてみる。
Ｐ波が出来たら、ＳＶ波放射特性(Rsv)も作成して、同じように確認して。
【1-2】地表での反射波（pP）と変換波（sP）を考慮して、E(t)を作成する
E(t)をgnuplotで図にして、出てくる結果を確認。
【演習2】震源の時間関数S(t)を作り、本堂でのE(t)*S(t)を計算する
【2-1】震源の時間関数S(t)を計算するプログラムをつくり、動作を確認
S(t)をgnuplotで図にして、出てくる結果を確認。
【2-2】出来たS(t)を計算するプログラムを使って、E(t)*S(t)を計算させる
E(t)*S(t)をgnuplotで図にして、出てくる結果を確認。
【演習3】非弾性減衰の効果P(t)をいれる
時間の余裕にあわせて、以下２つから、どちらかを選択して行う。
◇時間に余裕のある人（３回目の演習や４回目開始時にこの項目に達した人）
【演習2】の出来上がりの波形にフーリエ変換を行って、 周波数領域の中で、非弾性減衰の効果を掛け、 結果を逆フーリエ変換で時間領域に戻すように、 【演習2】で作ったプログラムを改良してください。 t*は１秒を使ってください。
フーリエ変換のプログラムはfcoolr.f
メインプログラムから
integer:: n
complex:: f(2048)
real:: rind
call fcoolr( n, f, rind )
のようにして呼び出すことができます。
ここで、配列fに含まれるデータは(2のn乗)個。 フーリエ変換ではrind=-1、逆フーリエ変換ではrind=1となります。 フーリエ変換のとき、変換された結果は、(2のn乗)倍になっていますので、 注意してください。
コンパイルの仕方は
gfortran メインプログラムのファイル名 fcoolr.f
です。
逆フーリエ変換した後、実数部にだけデータがある（虚数部がゼロ）ためには、 周波数領域の複素データが、折り返し点をはさんで、 後半部と前半部で共役になっていることが必要です。 非弾性減衰を前半部の複素データに作用させ、 後半部をその共役な値で埋めることにより、これを実現します。
例えば、以下のような周波数領域で１６の複素データをもつ場合、 ９つ目のデータが折り返し点になります。 この折り返し点をはさんで前後のデータを共役にします。
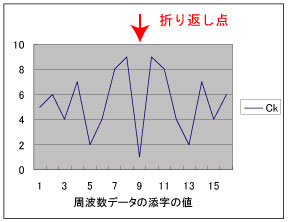
上のFFTのプログラムでは、周波数領域でi番目の複素データ（前半部）は、
(i-1)/データ長
の周波数に対応します。
（ここで、データ長は、時間ステップ（△t）かける２のｎ乗です。)
◇時間に余裕のない人
非弾性減衰の応答関数として、デルタ関数に対する t*=1秒の場合にえられる時間関数（時間ステップ△t=0.2秒）を ココ におきました。このデータをプログラムで読み込み、 時間領域で畳み込み積分して、非弾性減衰の効果をいれてください。
(2) その結果をもとにしながら、 断層の走向、傾斜角、すべり角、ずれの継続時間や時間関数、 深さをどのように変えると、計算波形と本堂での観測波形が似るようになるかを調べる。
2011年1月14日（金）締め切り
Wordファイルかpdfファイルにまとめたものを久家宛にメールで送ってください。
メールの件名（サブジェクト）を「ＤＣレポート」にしてください。
レポート内には、名前を忘れずにいれてください。