フーリエ変換のサブルーチンはfcoolr.f

このフーリエ変換のサブルーチンを使うには、 メインプログラムの中に、次の３つの定義文をいれます。

integer:: n
complex:: f(8192)
real:: rind

その上で、 配列fの実数部に、時系列データの値を入れます。
必要に応じて、データにテイパーやウィンドウをかけます。
配列fの虚数部はゼロにします。

そして、メインプログラムで

call fcoolr( n, f, rind )

のようにして呼び出すことで、FFTを走らせることができます。
この文のあと、配列fにはFFTの結果が入っています。

FFTは、データ数を2の累乗個にすることで、高速化を実現しています。 データ数は整数nの値によって決まり、 配列fに含まれるデータ数は(2のn乗)個になります。

実数rindの値がフーリエ変換か逆フーリエ変換かを決めます。 フーリエ変換ではrind=-1、逆フーリエ変換ではrind=1となります。

フーリエ変換のとき、変換された結果は、(2のn乗)倍になっています。 (2のn乗)で割ることで正しい値になります。

メインプログラムのコンパイルの仕方は

gfortran メインプログラムのファイル名 fcoolr.f

です。 メインプログラムと同じdirectoryにダウンロードした fcoolr.fをおいてください。 メインプログラムへfcoolr.fの内容を貼り付ける必要はありません。

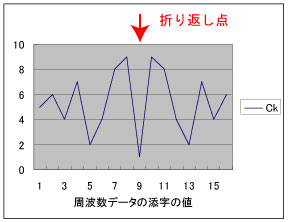
時系列データからフーリエ変換で作成された周波数領域の複素数データは、 折り返し点（折り曲げ点）をはさんで前後半で共役になっています。

例えば、16つの時系列データをフーリエ変換すると、 周波数領域における16つの複素数データfが得られます。 ９つ目のデータが折り返し点になっていて、 この折り返し点をはさんで配列fの前後半のデータは共役になっています。

上のFFTのプログラムでは、周波数領域でi番目の複素データf（前半部）は、

(i-1)/データ長

の周波数(Hz)に対応します。
ここで、データ長（秒）とは、 元の時系列データの時間間隔（△t）×データ数（２のｎ乗）にあたります。

この周波数における振幅は

|f(i)|

位相は

f(i)の偏角　arg f(i)

となります。
arg f(i)は、atan2( f(i)の虚部、f(i)の実部 ）で計算できます。