【ステップ２】

本日の計算地球物理学入門（講義）で述べたように、 周波数が高い地震波では、地震波は波線の方向へ伝播していくと 近似できます。 この地震波の波線は、光と同じように、スネルの法則 （Snell's law）に従って、地球の中を伝播していくと考えることが できます。 このスネルの法則とは、同じ波線上では、入射角と地震波速度の間に、 一定の関係が成り立つというものです。

例えば、地震波速度の異なる２つの層がある場合、地震波の波線は 次の矢印のついた線のようになります。

２つの層を通過している波線で成り立っているスネルの法則は、

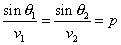
ここで、ｐは、ray parameterと呼ばれる量です。同じ波線の上では、 このｐの値が一定となるように地震波が伝播するというわけです。

今回の演習では、このスネルの法則と波線の関係を、下の図のように、 もっとたくさんの層からなる場合で考えてみましょう。

深くなるにつれて地震波の伝播速度がはやくなるようになっていると、 地震波は、地表から地下へと伝わり、また、地下から地表に戻ってきます。

今回は、地震を起こした断層が非常に小さくて、地表（深さ０ｋｍ）にあると仮定します。 このとき、 地震波が地表に戻ってくるまでに水平方向に伝播する距離、 地震波が地表に戻ってくるまでに要する時間（走時といわれます）は、 以下のように与えられます。

シグマの内にはいっている式は、上式では、 各層（i番目の層）内を通過する波線が水平方向にすすんだ距離、 下式では、 各層（i番目の層）を伝わるのに要した時間になっています。 ２倍しているのは、地下深部に向かって伝播するときと、地表に戻ってくるときと、 同じ層を２回通るからです。今回の演習は、これらの式を使います。

さて、速度構造１を使って、地表から地下にむけて、鉛直から３０度で入射する 地震波の場合の計算方法について、以下に説明します。まず、計算の仕方を 理解してください。

今回の演習では、皆さんは、速度構造２で計算を行ってください。 そして、皆さんが得た結果が、以下最後にでてくる速度構造１の 図とどう違うか、比較してください。 速度構造２ができたら、速度構造３をやってみてください。

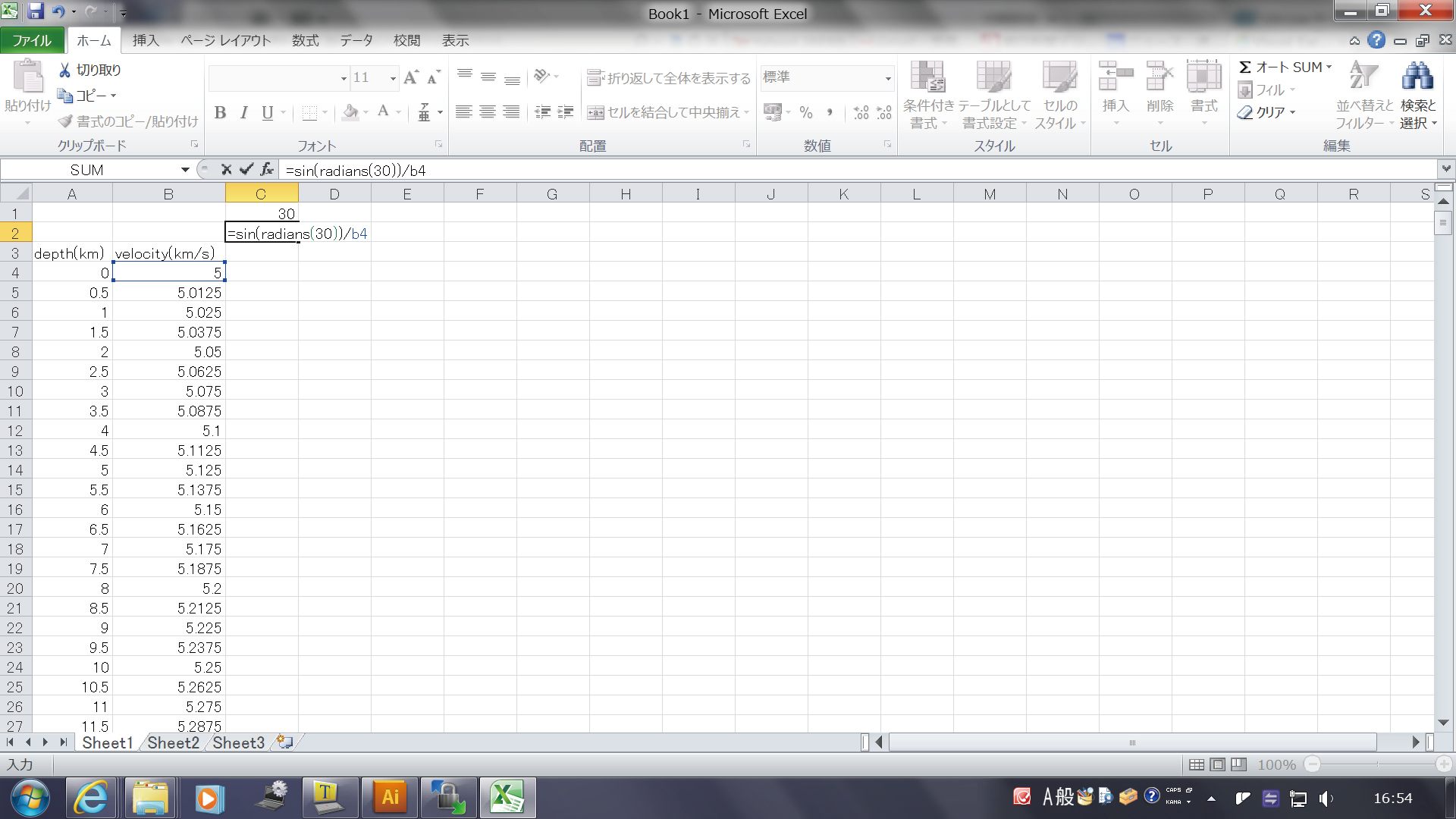
深さと速度のデータを読み込んだシートにいきます。 まず、入射角（表層で波が入射する角度）と ray parameter（ｐ）の値をいれておくために、 先頭行に、新しい行を２つ追加します。 これは、行をしめす「１」を選んだ後、「挿入」「行」で行えます。

わかるように、Ｃ１のコラムに入射角を書いておきましょう。 ここでは、３０（度）です。 Ｃ２のコラムに、ray parameter（ｐ）の値を計算します。 ray parameter（ｐ）の定義式を入力します。B4は入射した地表層での 地震波速度です。

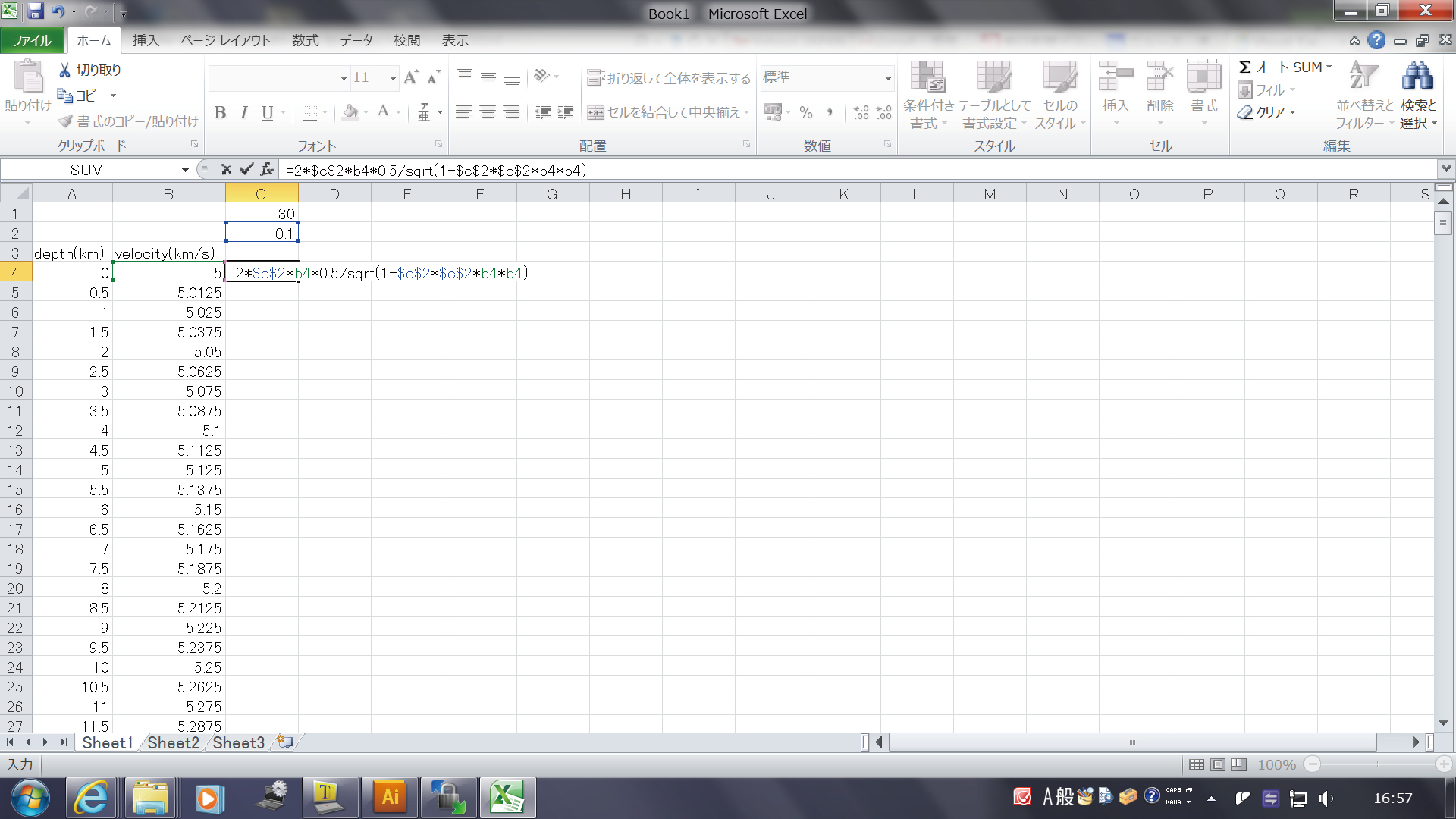
さて、計算した部分を下の方にたどっていくと、途中で 数値のかわりに#NUM!という文字がでてきます。 距離を計算する式の中に、ルートを計算するところがあります。 深さが深くなって速度が大きくなってくると、あるところで、 ルートの中が負の値になります。 #NUM!はそのことを示しています。この層には、地震波の波線は ありません。この層の上端で、地震波の波線は、下向きから上向きに 変わります。

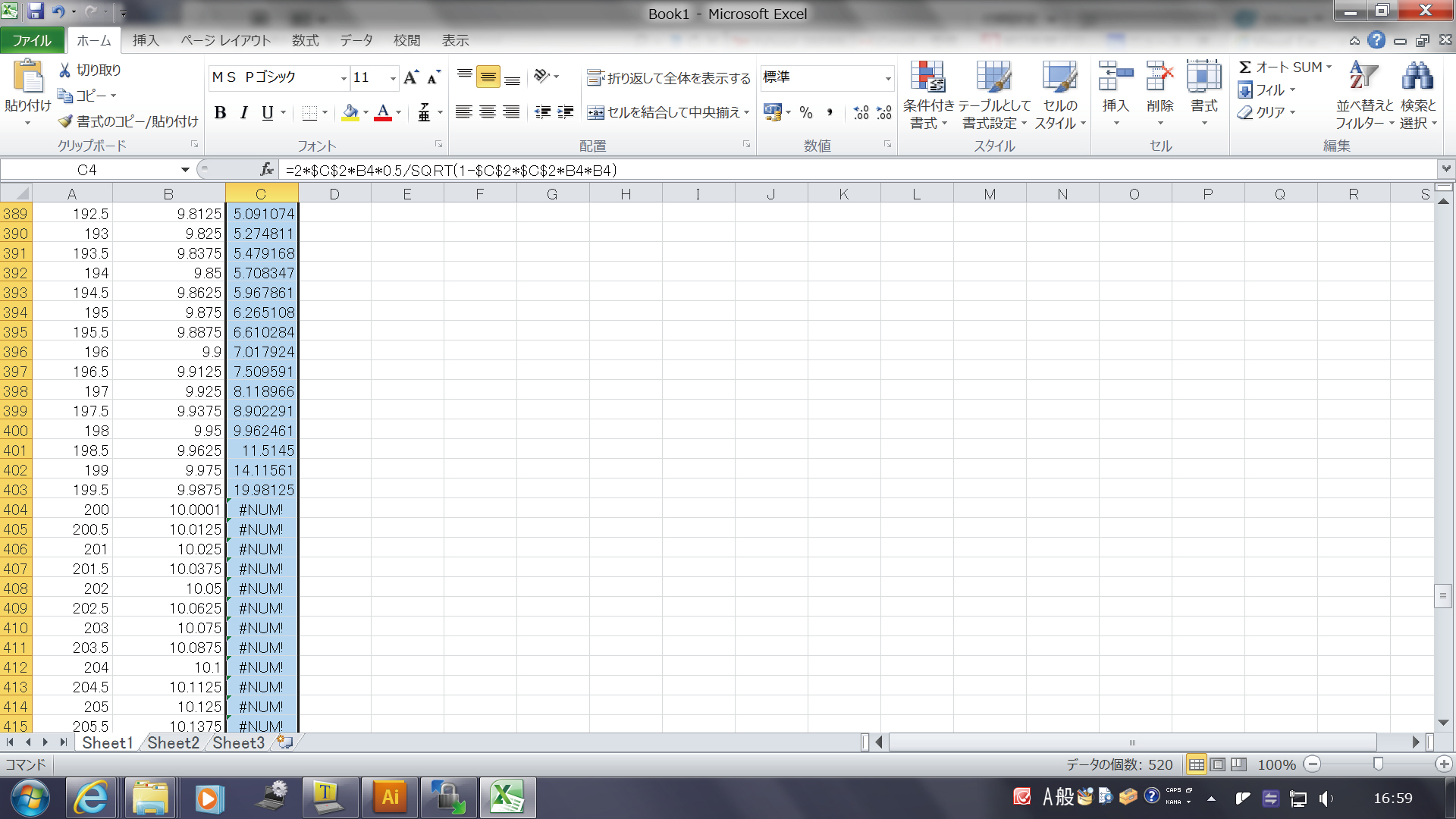
計算できたら、枠の右下を下にひっぱって、 下の行についても、同様に計算させます。

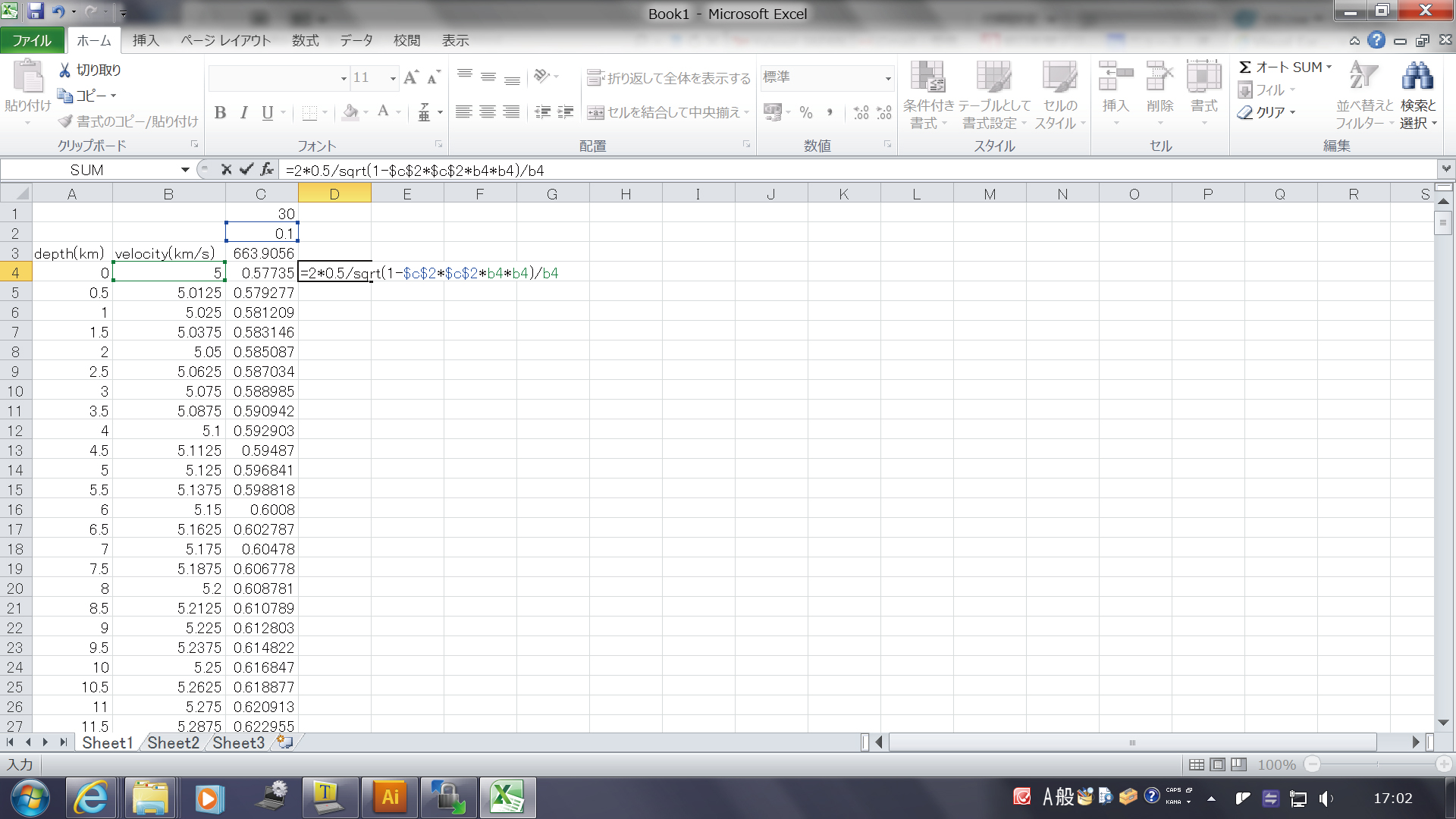
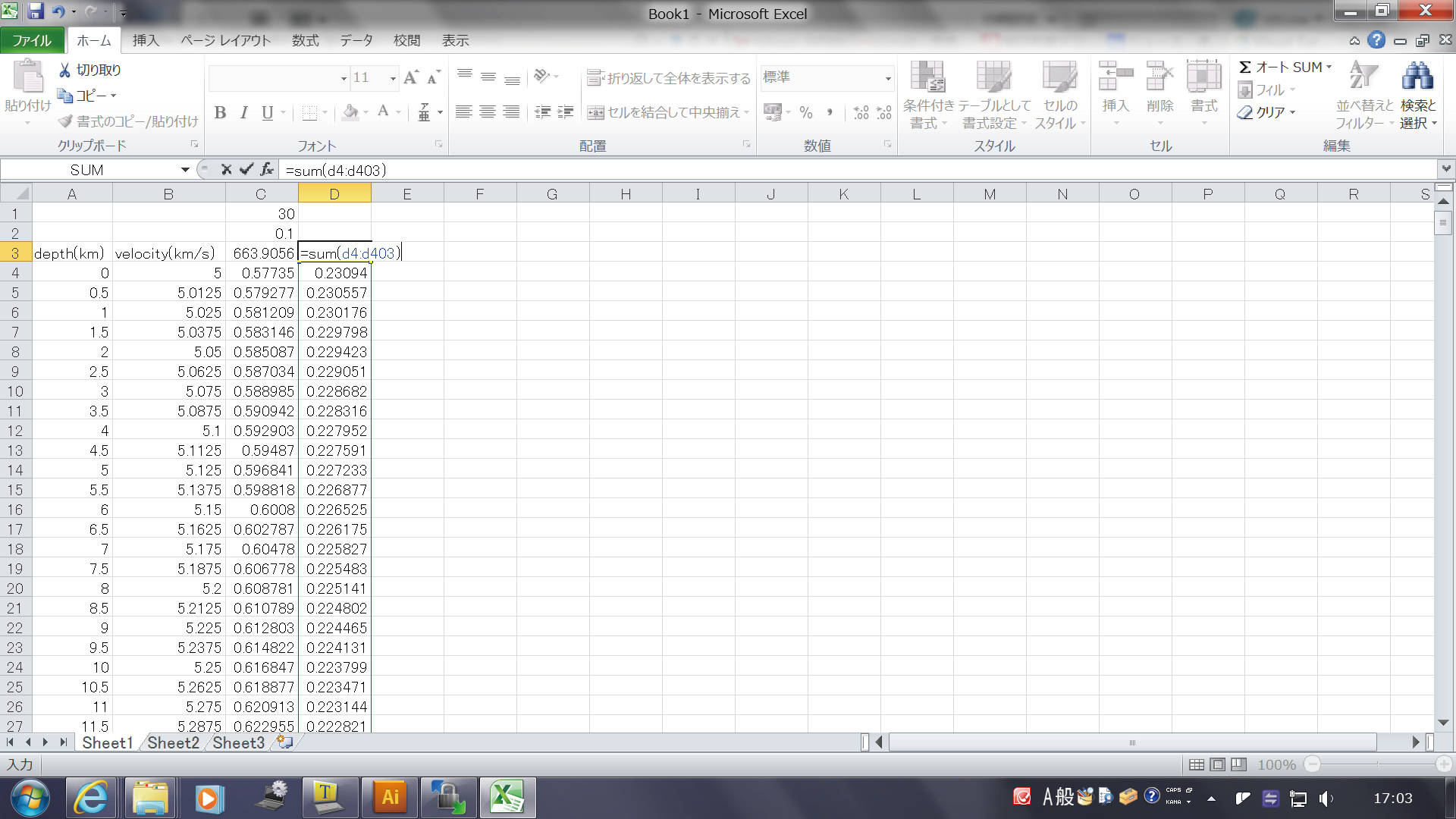
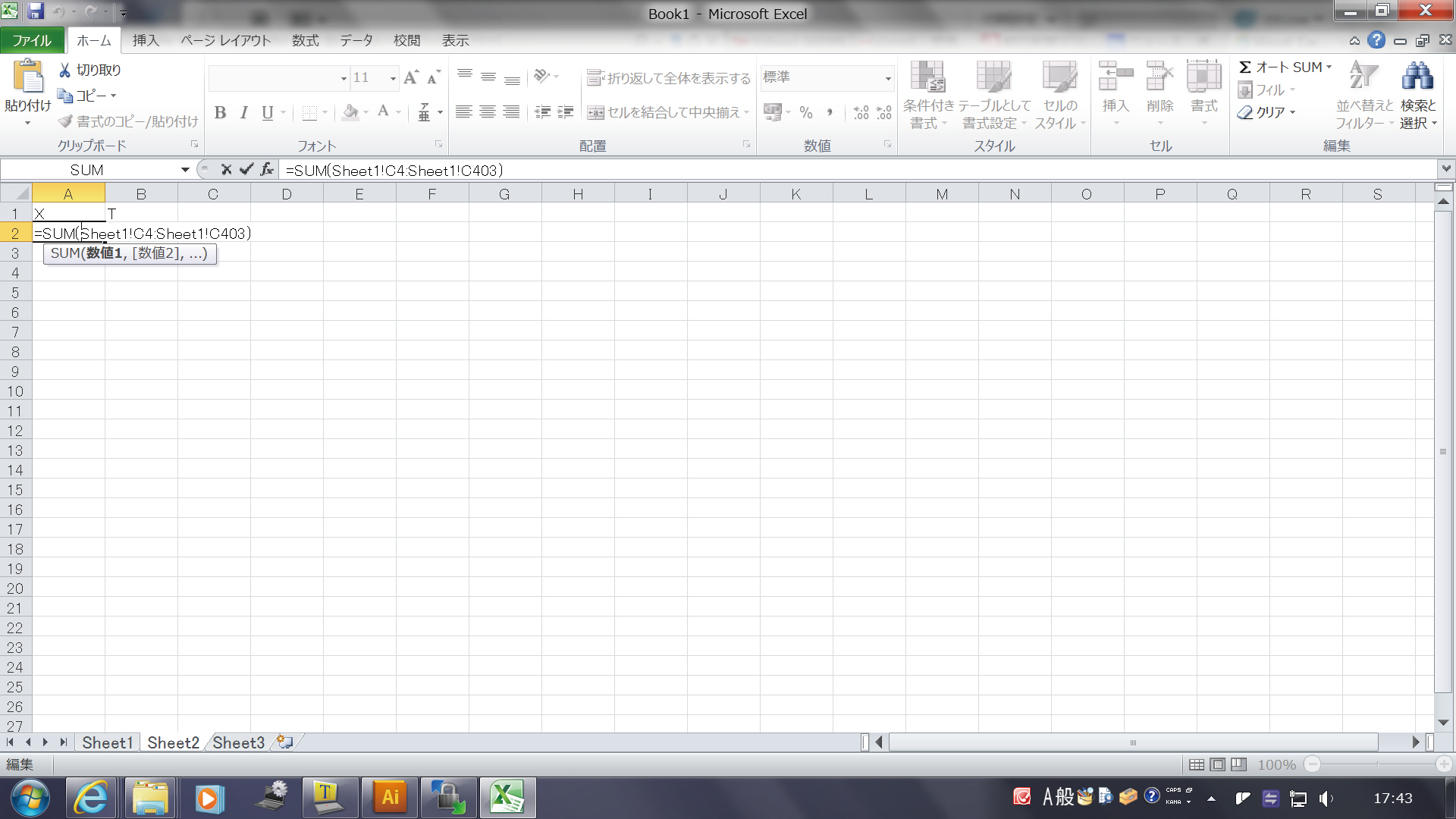
このとき、下のように、シートの名前を指定した形で、 数式をコラムの中に書いてあげることによっても、 別のシートの上に数式の結果を移すことができます。

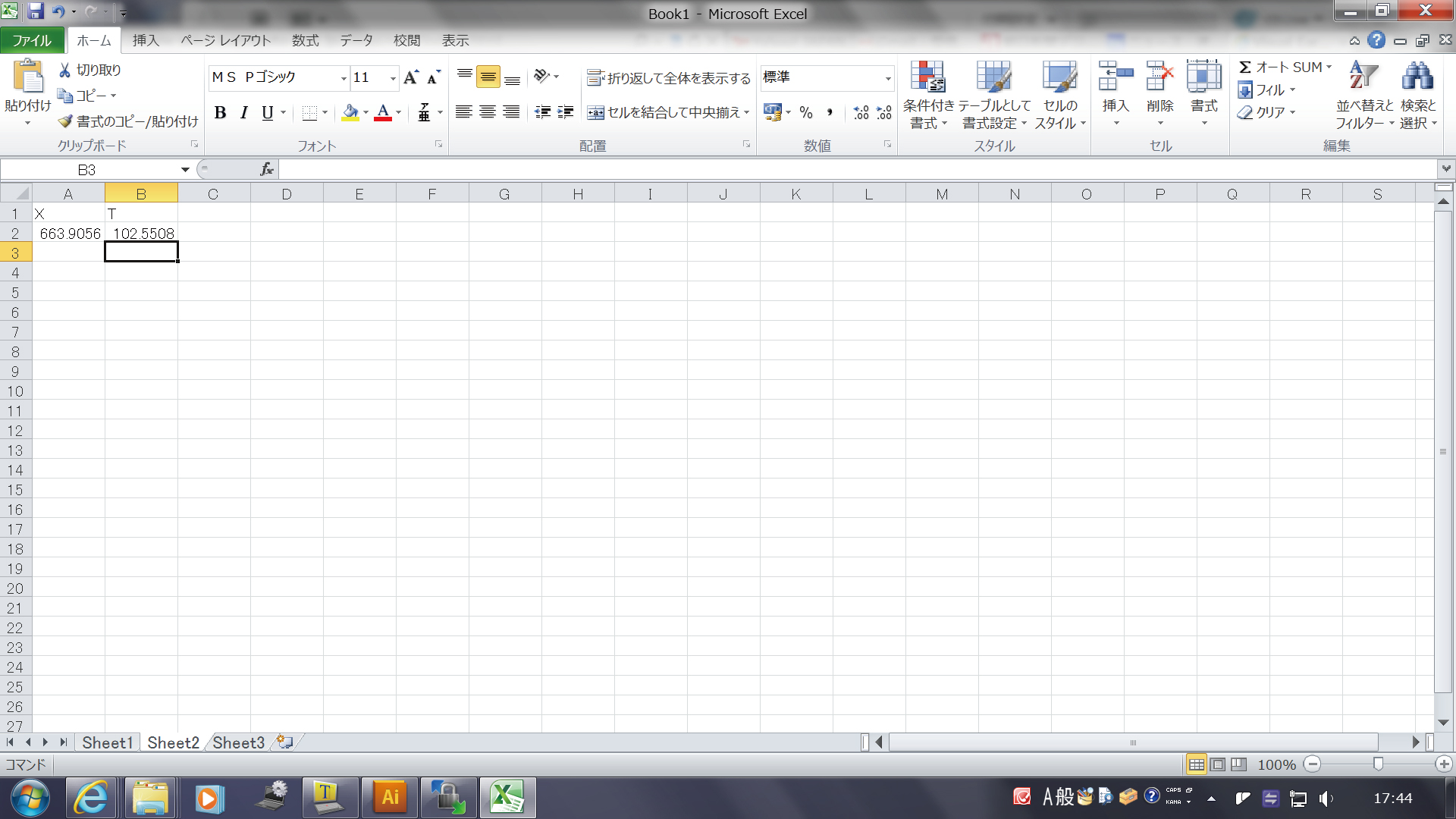
まとめた表を使って、横軸に水平距離、縦軸に走時になるようにして、 「散布図を折れ線でつなぐ」グラフで描いたものが下です。 地震波が地中の中を伝わって遠くまで達するにつれて、 かかる時間も単調に増加しているようすがみられます。

いずれの速度構造でも、 地表での射出角は、３０度から４４度まで、２度間隔で、試みてみてください。

速度構造２の場合には、速度構造１と同じように、 「散布図」のうち線でつないだグラフを使うと、特徴がよくわかります。

一方、速度構造３の場合には、線でつながず点 の散布図のグラフでみると、特徴がよくわかります。