日本列島には、約1300点のGEONET(GNSS連続観測システム)の電子基準点が設置され、 その位置が時々刻々と観測されています。
国土地理院の基準点・測地観測データのホームページ (http://www.gsi.go.jp/kizyunten.html)で、 誰でもそのデータをダウンロードできます。この位置データをもとに、 日本列島が今どのように変形しているのかを知ることができます。

今回の演習では、このデータをもとに、 2011年3月11日東北地方太平洋沖地震前・時・ 後の東北地方の変形を調べます。
【演習1】地震前の東北地方の変形
(1) まず、新潟と山田、新潟と小高、新潟と本荘の間の距離の変化を、 それぞれ、グラフにしてください。 期間は、1997年から1999年の3年間です。 横軸に日数、縦軸に2点間の距離の変化量(1997年1月1日の距離を基準とする) となるグラフです。
(2) 更に、(1)のグラフの変化量を各々の基準となる距離で割って、 距離変化率の日変化のグラフにしてください。 この距離変化率は、法線(垂直)ひずみにあたります。 できた図を使って、 1年間の垂直ひずみの変化量、つまり「ひずみ速度」の平均的な値も、 3つそれぞれの場合で見積もってください。 あわせて、この値を使って、 講義で北丹後地震に見積もった程度の地震によるひずみ変化をためるためには、 何年間必要となるか、計算してください(電卓で可)。
(3) (2)で推定した1年間の垂直ひずみ(「ひずみ速度」)の値を 3つの場合で比較し、方向とどのような関係になっているか、 みてください。
【演習2】地震時および地震後の東北地方の変形
(1) 【演習1】(1)と同じように、2011年から2013年までの新潟と山田の間の距離の変化量をグラフにしてください。
東北地方太平洋沖地震時の距離の変化がどれにあたるかをみつけてください。
東北地方太平洋沖地震前と地震時の距離の変化のようすは
どのように違うかをみてください。
(2) 東北地方太平洋沖地震直後から2013年末までの距離の変化が、
地震時の変化の何パーセントになるかを計算してください(電卓でもよいです)。
地震後の変形は、「余効変動」と呼ばれるものです。
2015年末には地震直後からの距離の変化は、
地震時の変化の何パーセントになっていると予想しますか?
予想する方法を考えてください。
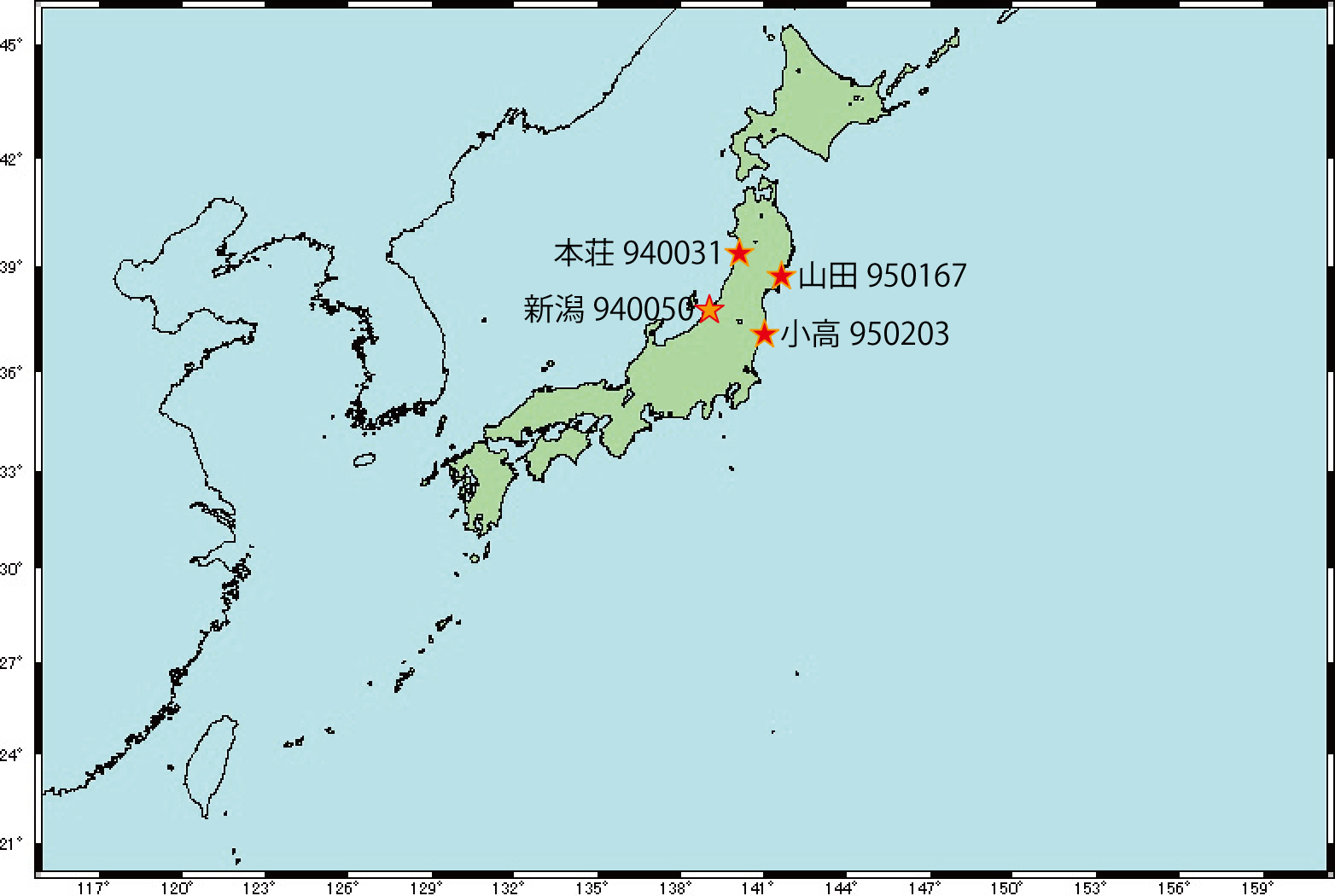
【演習1】【演習2】に必要なデータは以下にあります。 前もって国土地理院のページから取得した 電子基準点の日々の座標変化のデータを用います。 各観測点で、1年間のデータが1つのファイルに入っています。
新潟(940050)
1997年 940050.97.pos
1998年 940050.98.pos
1999年 940050.99.pos
2011年 940050.11.pos
2012年 940050.12.pos
2013年 940050.13.pos
山田(950167)
1997年 950167.97.pos
1998年 950167.98.pos
1999年 950167.99.pos
2011年 950167.11.pos
2012年 950167.12.pos
2013年 950167.13.pos
小高(950203)
1997年 950203.97.pos
1998年 950203.98.pos
1999年 950203.99.pos
本荘(940031)
データの先頭には、
+DATAの下の部分が、今回使うデータです。 使わない先頭の部分を削除します。
また、ファイルの最後にも、余分な部分があるので削除し、保存します。
ここでは、2005年の1年間のデータを使って、新潟と山田の間の距離の変化を
調べる場合を例にして、作業を説明し
ます。
皆さんは、【演習1】の作業に続けられるように、
1997年の新潟と山田のデータを使って、作業してみましょう。
先週の演習にならって、
余分な部分を削除した
新潟のテキストデータをExcelに読み込んでみましょう。
忘れてしまった人は、
先週のホームページを見直してみてください。
さて、読み込んだ数値で計算をしてみましょう。
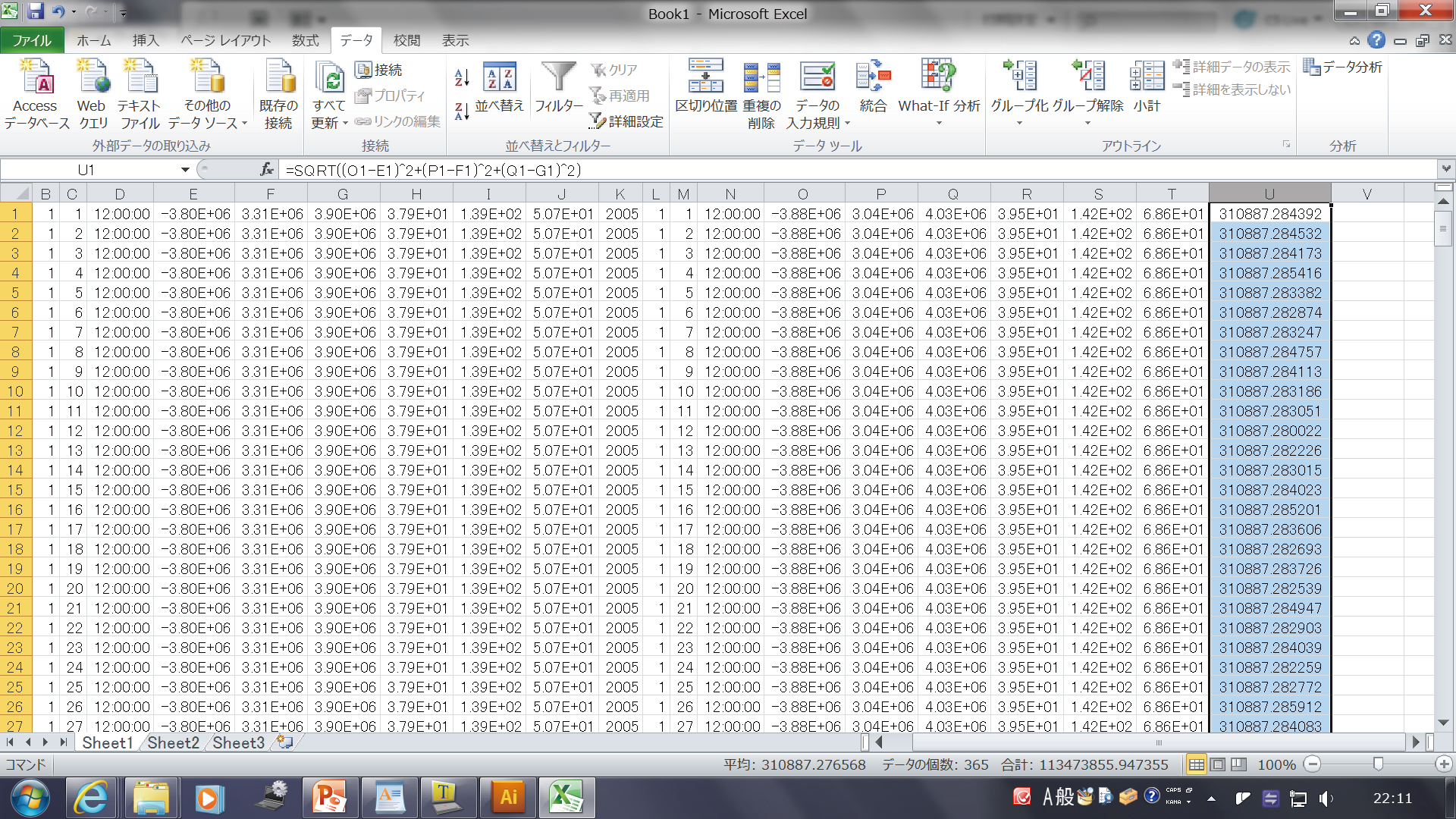
2005年1月1日の新潟の観測点の位置は、X,Y,Z座標の値として、
1行目のE列、F列、G列に与えられています。
同じように、
山田の観測点の位置は、X,Y,Z座標の値として、
1行目のO列、P列、Q列に与えられています。
この2つの観測点の間の距離は、
X,Y,Z座標での値の差の2乗和の平方根で計算できます。
その結果を1行目U列のコラムにいれるには、
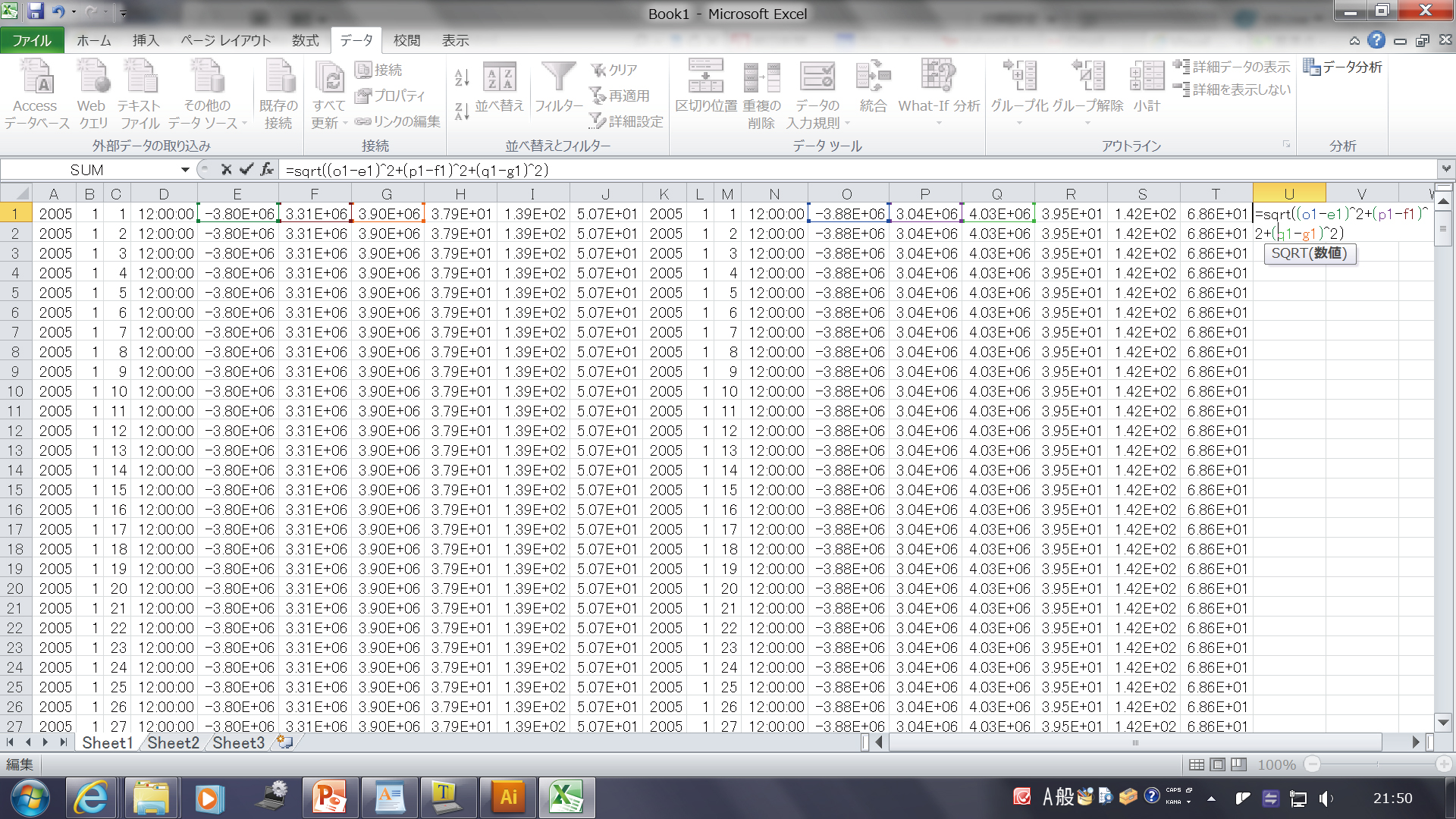
1行目のU列のコラムに、以下を入力します。
=sqrt((o1-e1)^2+(p1-f1)^2+(q1-g1)^2)
ここで、sqrtは平方根、^2は2乗を示します。
また、o1,e1は、O列1行目の値、E列1行目の値を意味しています。
入力したあと、Enterを押せば、計算結果が自動的にはいります。
表示を変えたいときには、
Uの部分を右クリックして、「セルの書式設定」を選択してください。
表示形式を「数値」に変更すると、小数点以下の桁数を指定できるようになります。
U1を選択して、その右下をずっと下にのばしてください。
すると、下の行にも値がはいります。計算された値は、例えば、
o1とe1の値にかわって、
各行の該当するO列とE列の値を使って、同じ式で計算した結果です。
確認するには、コラムを2回クリックしてください。計算している式が現れます。
もし、いつでも同じコラムの値を使う(絶対参照)には、
$K$10という具合に、行と列の番号の前に$をいれます。
計算ができたら、
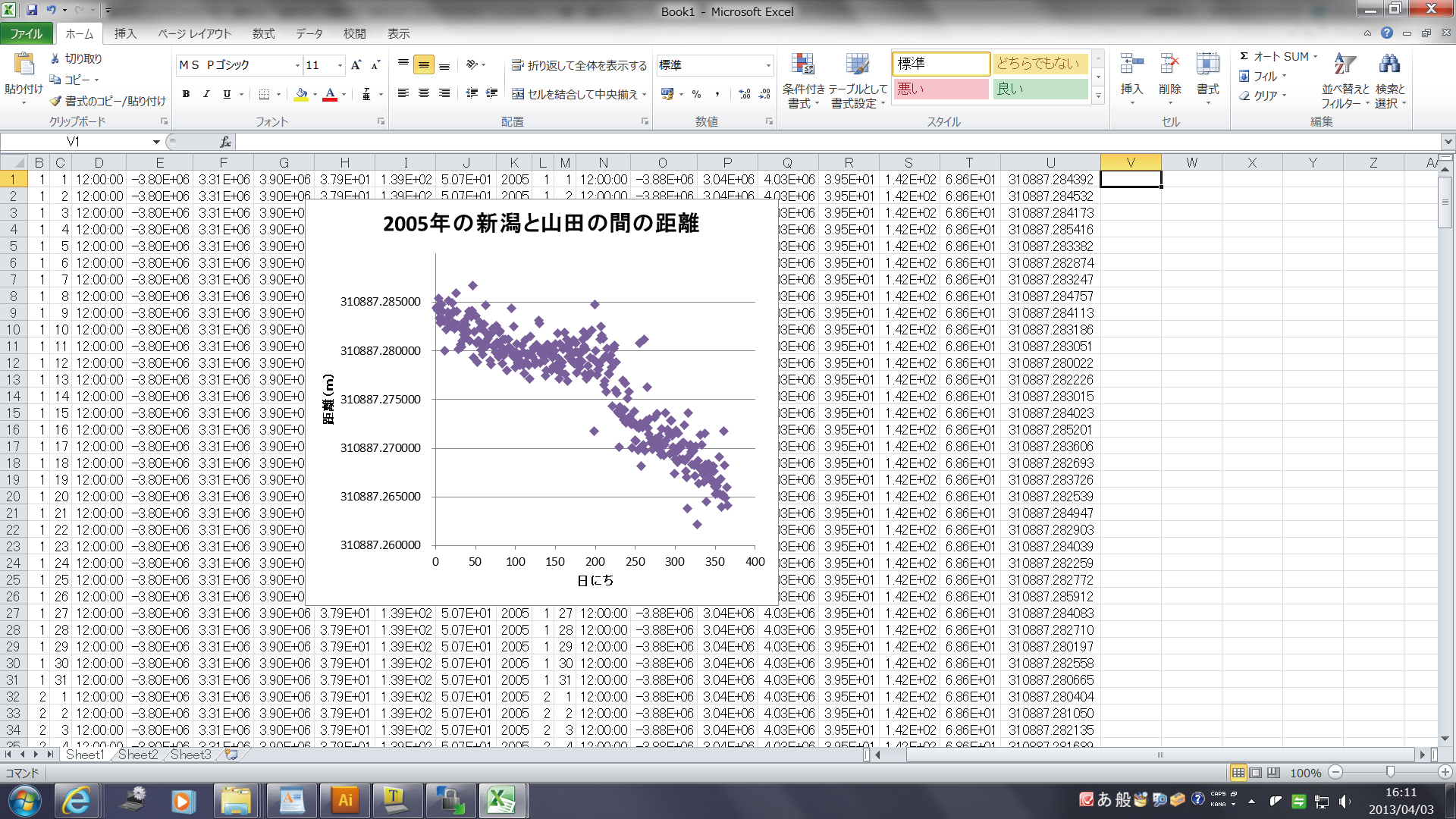
横軸に日数、縦軸に2点間の距離となるグラフを
作成してみましょう。グラフの描き方は、先週やりましたね。
2005年1年間の距離の変化は以下です。
データの数が多いためか、エクセルがうまく働かないときがあります。
エクセルの挙動が不安定な場合、
作成した図の上で右クリックし、「グラフの移動」「新しいシート」を選択し、
グラフを別のシートに移すと、エクセルの挙動は幾分安定します。
さて、これで、距離の計算の仕方とグラフの作り方がわかりましたね。
では、引き続き、【演習1】【演習2】をやってみましょう。
1997年 940031.97.pos
1998年 940031.98.pos
1999年 940031.99.pos
・ 観測点番号(ID)
・ 観測局名(F_NAME)
などが書かれています。
・年月日(yyyy mm dd)
・地球の重心を原点とした地心座標系での X,Y,Zの値(単位はメートル)
を含めた数値が、1日1行、1年分並んでいます。